ToDoリスト

仕事を効率よく進めるためにToDoリストを作成している人は多いかもしれません。

やるべき仕事を視覚化することで漏れをなくし、優先順位も見直すことができますので、便利なツールだと思います。

そこで今日は私のToDoリストの使い方を紹介したいと思います。

■榊原慎太郎のToDoリスト（内容は若干変えてあります）


使い方はいたってシンプルで、単にやるべきことを書き出して実施した項目を塗りつぶすというものです。
左側の日付は記入した日付で、右側は実施した日を表します。

やるべきことが思いついたら、その都度下に書き足していきます。
１日に複数思いつくこともあれば、ゼロという日もあります。

上のリストからは、２つの項目しか処理されていないことがわかります。
また、取消線が引かれている項目は、もう処理する必要がなくなったことを表します。

あと、絶対という訳ではありませんが、私の場合は必ずやらなければならないことというよりは、やった方がいい、というレベルのものを中心に書き出すようにしています。

必ずやらなければならないことは絶対やる訳ですし、期限が決まっているものがほとんどですからリスト化する意義はそんなにないと思っています。

それよりも、期限がある訳ではなく、やっておいた方が後々プラスになる、あるいはやらないと困ったことになるようなことを書き出すようにしています。

「家族旅行の計画を立てる」というのは典型かと思います。

一番上の「メールを送る」という項目についても、私の場合は何かに対するお礼のメールが多くを占めます。
お礼のメールというのは送らなければならないものとは言えません。

どうするかはその人の自由であります。
しかし、今後も関係を保っていきたいと考えるなら送っておいた方がいいという判断になるでしょう。

あと、特徴と言えるのは「セミナーに参加する」ではなくて「セミナーに参加するかどうか決める」という表現になっていることでしょうか。

もし、セミナーに参加するとなれば、それはToDoリストではなくスケジュール帳へ記入すべき項目になるからです。

そして、そのセミナーに向けて準備しておくことがあれば、さらにリストに追加することになります。
参考になれば幸いです。


↓応援のクリックお願いします。


人気ブログランキングへ

いつもありがとうございます

close

売り物で勝負するか売り方で勝負するか②

（昨日の続きです）

■昨日の記事


韓国に限って言えばウォン安の恩恵を受けた面もあるでしょうが、総じて海外勢の製品が日本製品と遜色ないレベルに高まったことが要因と考えられます。

大して変わらなくなってしまったということです。

そうなりますと、製品自体のアドバンテージはなくなったも同然であり、マーケティングすなわち売り方が勝負の行方を左右することになろうかと思います。

液晶テレビに関して言えば、韓国メーカーは非常に巧みだったと言えるのではないでしょうか。

ただし、ある特定の部品といったマニアックな製品では相変わらず日本企業が高いシェアを持っている場合があります。
そのような企業は、売り物で勝負していっても構わないと思いますが、だんだん少なくなっていくだろうと考えられます。

これから私達はどのように売っていくかということを真剣に考えねばならないでしょう。

ブルーレイが登場して何年か経ちましたが、私は未だにブルーレイの映像を見たことがありません。
友人でブルーレイプレーヤーを買ったという話も聞いたことがありません。

よい製品が必ず売れるという時代ではなくなってしまったということなのだと思います。
売り物以上に売り方を重視することが肝要と言えそうです。

↓応援のクリックお願いします。


人気ブログランキングへ

いつもありがとうございます

売り物で勝負するか売り方で勝負するか

高度成長期の日本は売り物で勝負していたと思います。
高い技術力を背景にした高品質な製品をどんどん輸出していきました。

今でも品質の高さという点では日本製品に分があるように思いますが、必ずしもマーケットシェアを拡大できていません。
アジアをはじめとした旺盛な消費地域があるにもかかわらずです。

液晶テレビなどはその典型と言えるでしょう。
今や液晶テレビは韓国勢に大きく水をあけられてしまいました。


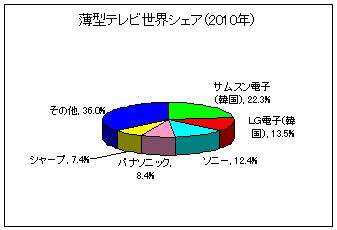
（「米ディスプレイリサーチ」より）

どうしてこんなことになってしまったのでしょうか。
明日に続けます。


↓応援のクリックお願いします。


人気ブログランキングへ

いつもありがとうございます

仲間を貯蓄しよう

私達３０代に限らず、せっせと貯蓄をしている人は多いと思います。
私もできる限り節約し、貯蓄したいと思っています。

しかし、過度の節約志向はいかがなものか、とも思っています。
特に仲間との関係を広げ、深めていくための費用は出し惜しみすべきではないというのが私の意見です。

これはかえって将来に憂いを残すことになるのではないでしょうか。

仲間と会って食事でもすればそれなりの費用がかかるものです。
しかし、それを惜しんで誘いを断るようなことをすればどうなってしまうでしょうか。

一度ならまだしも何度もそれが続けば、やがては誘ってもらえなくなり、関係さえも消滅してしまうかもしれません。
貯蓄すべきはお金よりも仲間であるということを肝に銘じておきたいものです。





↓応援のクリックお願いします。


人気ブログランキングへ

いつもありがとうございます

官僚は本当に優秀なのか

これは最近疑問に感じていることでありますが、官僚は本当に優秀なのでしょうか。

本当に優秀だったのなら、どうして1,000兆円もの借金を積み重ねてしまったのでしょうか。
それとも、優秀な彼らだったから1,000兆円で済んでいると考えるべきなのでしょうか。

それなりに人生経験を積んだ人なら理解していると思いますが、優秀であることが善良であるとは限らないということだと思います。
むしろ優秀であるが故に胡散臭さも付きまとうのが、官僚批判の根底にあるような気さえいたします。

これから官僚に求められる資質は、優秀であることに加えて善良であることが重要になってくると思います。

国民に対して良い行いをした、

そう心から言える官僚が現れてほしいと願わずにはいられません。


↓応援のクリックお願いします。


人気ブログランキングへ

いつもありがとうございます